
This is often used to calculate the area of a triangle. The length of a perpendicular from a side of the triangle to the opposite vertex. An interesting fact is that the three altitudes always pass through a common point called the orthocenter of the triangle. an altitude may be referred as a line segment which passes through any vertex and forms the right angle with the edge opposite to this vertex.Īn altitude is a line which passes through a vertex of a triangle and meets the opposite side at right angles. The altitude of a triangle is defined as a perpendicular drawn from any vertex (a point where two sides of a triangle meet) on to the opposite side (base)of that triangle, i.e. Since a triangle has three sides, hence it can have three bases. It is a special case of orthogonal projection.įig: Some examples of the altitude of a triangleĭefinition: Any side of a triangle can be assumed as its base.

The process of drawing the altitude from the vertex to the foot is known as dropping the altitude at that vertex. The length of the altitude, often simply called “the altitude”, is the distance between the extended base and the vertex. The altitude is the shortest distance from a vertex to its opposite side. A triangle, therefore, has three possible altitudes. The intersection of the extended base and the altitude is called the foot of the altitude. This line containing the opposite side is called the extended base of the altitude. Sometimes the opposite side isn’t quite long enough to draw an altitude, so we are allowed to extend it to make an altitude possible.
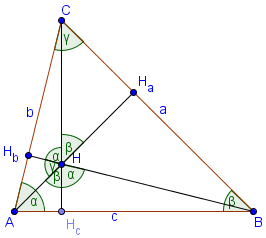
The definition of the altitude of a triangle is a line that extends from one vertex of a triangle perpendicular to the opposite side. In geometry, an altitude of a triangle is a line segment through a vertex and perpendicular to a line containing the base.


 0 kommentar(er)
0 kommentar(er)
